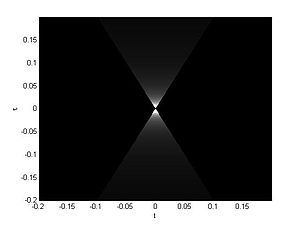
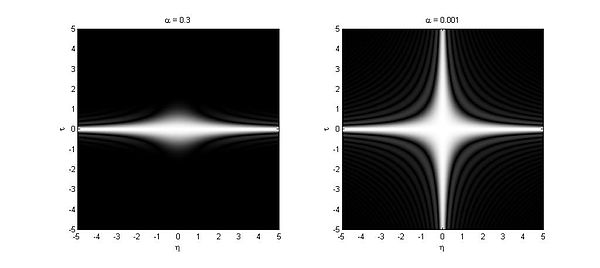
Cone-shape distribution function
The cone-shape distribution function, also known as the Zhao–Atlas–Marks time-frequency distribution,[1] (acronymized as the ZAM [2][3][4] distribution[5] or ZAMD[1]), is one of the members of Cohen's class distribution function.[1][6] It was first proposed by Yunxin Zhao, Les E. Atlas, and Robert J. Marks II in 1990.[7] The distribution's name stems from the twin cone shape of the distribution's kernel function on the plane.[8] The advantage of the cone kernel function is that it can completely remove the cross-term between two components having the same center frequency. Cross-term results from components with the same time center, however, cannot be completely removed by the cone-shaped kernel.[9][10]
Mathematical definition[edit]
The definition of the cone-shape distribution function is:
where
and the kernel function is
The kernel function in domain is defined as:
Following are the magnitude distribution of the kernel function in domain.
Following are the magnitude distribution of the kernel function in domain with different values.
As is seen in the figure above, a properly chosen kernel of cone-shape distribution function can filter out the interference on the axis in the domain, or the ambiguity domain. Therefore, unlike the Choi-Williams distribution function, the cone-shape distribution function can effectively reduce the cross-term results form two component with same center frequency. However, the cross-terms on the axis are still preserved.
The cone-shape distribution function is in the MATLAB Time-Frequency Toolbox[11] and National Instruments' LabVIEW Tools for Time-Frequency, Time-Series, and Wavelet Analysis [12]
See also[edit]
- Cohen's class distribution function
- Choi-Williams distribution function
- Wigner distribution function
- Ambiguity function
- Short-time Fourier transform
References[edit]
- ^ Jump up to: a b c Leon Cohen, Time Frequency Analysis: Theory and Applications, Prentice Hall, (1994)
- Jump up ^ L.M. Khadra; J. A. Draidi; M. A. Khasawneh; M. M. Ibrahim. "Time-frequency distributions based on generalized cone-shaped kernels for the representation of nonstationary signals". Journal of the Franklin Institute. 335 (5): 915–928. doi:10.1016/s0016-0032(97)00023-9.
- Jump up ^ Deze Zeng; Xuan Zeng; G. Lu; B. Tang (2011). "Automatic modulation classification of radar signals using the generalised time-frequency representation of Zhao, Atlas and Marks". IET radar, sonar & navigation. 5 (4): 507–516. doi:10.1049/iet-rsn.2010.0174.
- Jump up ^ James R. Bulgrin; Bernard J. Rubal; Theodore E. Posch; Joe M. Moody. "Comparison of binomial, ZAM and minimum cross-entropy time-frequency distributions of intracardiac heart sounds". Signals, Systems and Computers, 1994. 1994 Conference Record of the Twenty-Eighth Asilomar Conference on. 1: 383–387.
- Jump up ^ Christos,Skeberis, Zaharias D. Zaharis, Thomas D. Xenos, and Dimitrios Stratakis. (2014). "ZAM distribution analysis of radiowave ionospheric propagation interference measurements". Telecommunications and Multimedia (TEMU), 2014 International Conference on: 155–161.
- Jump up ^ Leon Cohen (1989). "Time-frequency distributions-a review". Proceedings of the IEEE. 77 (7): 941–981. doi:10.1109/5.30749.
- Jump up ^ Y. Zhao; L. E. Atlas; R. J. Marks II (July 1990). "The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals". IEEE Transactions on Acoustics, Speech and Signal Processing. 38 (7): 1084–1091. doi:10.1109/29.57537.
- Jump up ^ R.J. Marks II (2009). Handbook of Fourier analysis & its applications. Oxford University Press.
- Jump up ^ Patrick J. Loughlin; James W. Pitton; Les E. Atlas (1993). "Bilinear time-frequency representations: New insights and properties". IEEE Transactions on Signal Processing. 41 (2): 750–767. doi:10.1109/78.193215.
- Jump up ^ Seho Oh; R. J. Marks II (1992). "Some properties of the generalized time frequency representation with cone-shaped kernel". IEEE Transactions on Signal Processing. 40 (7): 1735–1745. doi:10.1109/78.143445.
- Jump up ^ [1] Time-Frequency Toolbox For Use with MATLAB
- Jump up ^ [2] National Instruments. LabVIEW Tools for Time-Frequency, Time-Series, and Wavelet Analysis. [3] TFA Cone-Shaped Distribution VI