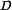Introduction
Reconfigurable
matching circuitry is needed in cognitive and adaptive wireless
transmitters for real-time changes in operating frequency and system
performance requirements. We designed a 1.3 GHz matching network using
the approach of Fu [1]
and used this to perform fast tuning of a field-effect transistor
(FET), optimizing gain using a fast steepest-ascent algorithm. Nemati
has demonstrated design of varactor-based tunable matching networks for
dynamic load modulation [2]. Qiao [3] and du Plessis [4]
have reported real-time impedance matching using genetic algorithms,
which tend to be inherently slow for many impedance matching problems.
We have previously demonstrated optimization of load impedance to
maximize output power [5].
This previous application of algorithms, however, is idealized in many
ways. In this paper, we implement the fast load-pull search to maximize
transducer gain 

Tunable Matching Network Design and Challenges
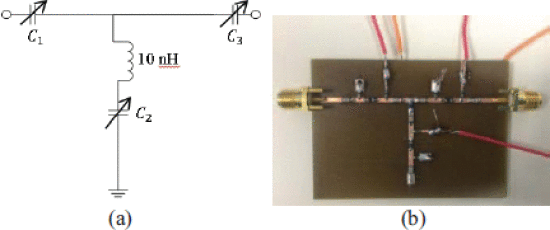
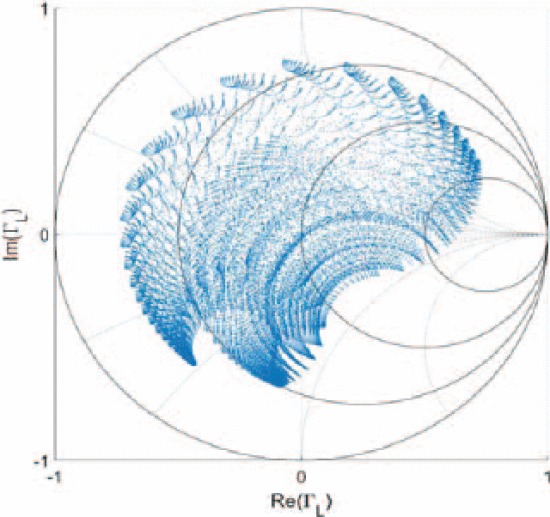
We designed a tunable-varactor matching network based on the method of Fu [1] at 1.3 GHz (Fig. 1(a)). The circuit was fabricated on a 59-mil FR4 substrate (Fig. 1(b)) and characterized at 0 dBm input power using S-parameter measurements (Fig. 2). The characterized range of the tuner covers much of the Smith Chart.
(a) Design of 1.3 GHz tunable matching network, based on Fu [1], (b) Implemented tunable-varactor matching network
Characterized load reflection coefficient states for the tunable varactor matching network
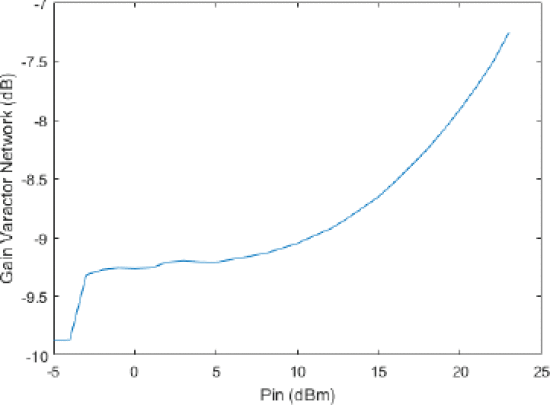
The tuner was also tested for nonlinear behavior. Significant
variations in the S-parameters with increasing input power are observed.
Figure 3 shows that at 



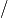
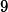
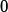








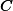


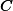

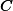



Algorithm Adaptation for Varactor Network
Our previous gradient search optimization [5] was modified and implemented with the tunable-varactor network to maximize 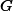

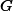












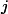
















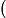
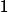
![]()



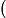
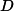


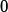
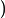
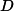





















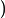

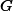



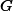


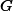


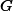





























![]()




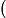

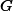

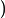











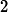
![]()





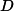

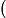

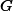


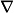
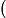

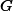

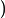


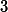
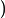
![]()
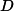

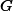

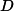

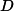

Measurement Results
The
algorithm was measurement tested using a Microwave Technologies MWT-173
FET, with single-tone input power of −20 dBm at 1.3 GHz. The small
input power value was used to ensure the varactor network is operated in
its linear region. Custom load-pull software was implemented for
matching and fixture network characterization and correction, as well as
communication with instrumentation. Figure 5
shows the −20 dBm loadpull characteristics as measured by the varactor
tuner, compared with contours measured by a standard Maury Microwave
tuner. The optimum 


1.3 GHz single-tone MWT-173 FET load-pull transducer gain 
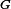




























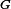

















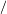








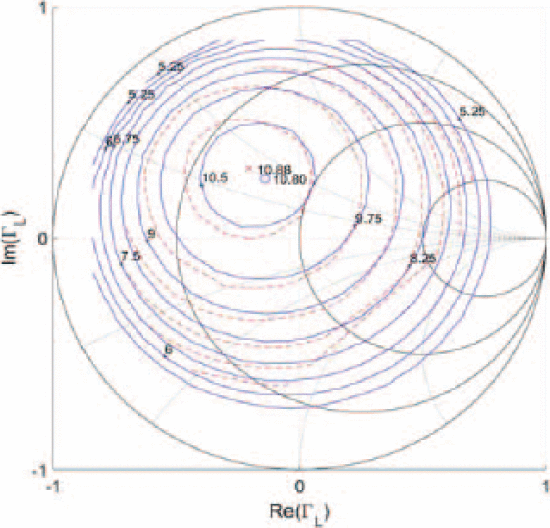
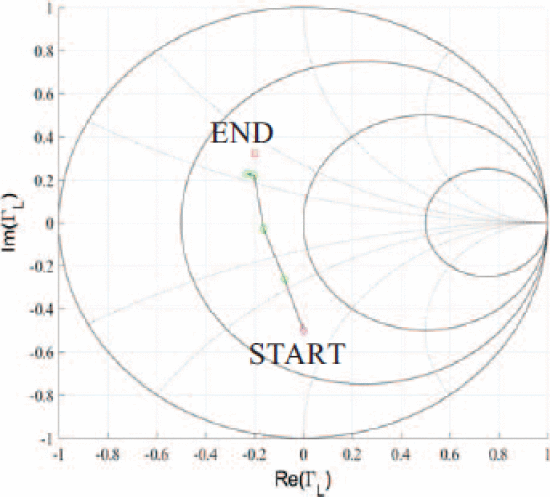
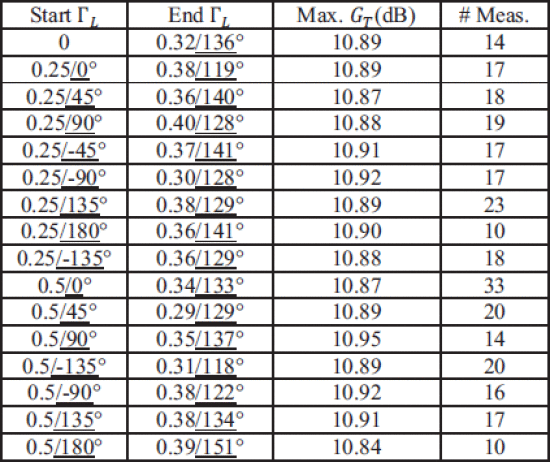
Figures 6 and 7 show two algorithm searches taken from different starting values of 



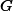



Even
for bench-top testing with significant equipment overhead, searching
with the varactor tuner is much faster than with the Maury tuner. An
algorithm run from 


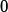
Fast load-impedance optimization for output power fromstarting location 




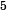













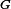





















Fast load-impedance optimization for output power from starting location 




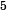





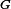






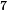


















Conclusions
A fast real-time load-impedance search algorithm has been demonstrated on a tunable-varactor matching network. The tunable-varactor network provides repeatable results from multiple starting reflection coefficients with a small number of measurements, comparing well with traditional load-pull measurements, but allowing fast, real-time reconfiguration. Results show excellent correspondence for different starting load reflection coefficient values, and compare well with traditionally measured load-pull results. This algorithm is expected to be useful for implementation in cognitive communication and radar systems, allowing the matching network to quickly adapt for changing frequency bands and performance requirements. Future work will investigate advanced power-dependent characterization to counteract the effects of matching-network nonlinearities.
ACKNOWLEDGMENT
This work has been funded by the Army Research Laboratory (Grant No. W911NF-16-2-0054) and the National Science Foundation (Grant No. ECCS-1343316). The views and opinions expressed do not necessarily represent the opinions of the U.S. Government.
Keywords
- IEEE Keywords
- Author Keywords