STEM Education 7: Sell the Sizzle
The mathematics underlying our world is fascinating and full of surprisesWe continue our discussion with the third of four principles necessary for STEM nerd parents and educators to bring the nerds to a healthy and fulfilling maturity. The first two, identification of nerds and nurturing them in the fundamentals, are here. Principle 3 is captured in the title above.
Advertisers long ago stopped listing impressive facts about their products. Outback Steak House does not tell us that the cows are contented or the butchers highly skilled. Instead, a commercial shows a freshly cooked steak on a platter, still sizzling from the grill. The steak is accompanied by a fully loaded steaming baked potato, dripping with melted butter. Rather than stating facts, the ad “sells the sizzle.” The art of sales is selling the anticipated experience.
Selling the nerd on STEM is similar but the sizzle can’t just be seductive optics. Those of us in STEM occupations love what we do but often fail to sell “honest” sizzle to aspiring STEM nerds. We must remember: Place a mountain between someone and a much-prized goal and that someone will climb the mountain. Sizzle helps establish a passion for the goal.
In my early days, I had to discover my own motivating sizzle. My STEM teachers were competent but never conveyed enthusiasm. The sizzle came from elsewhere. One of my favorite shows as a kid was Mr. Wizard, which offered fascinating science. What happens when two identical balloons are inflated to different sizes and their stems are connected so that the air from one is allowed to flow into the other? The answer is contrary to what most people predict: The less inflated balloon empties into the more inflated balloon. I found it all fascinating.
One of Mr. Wizard experiments had a huge impact on my life. Mr. Wizard showed how to drive a common sewing needle through a dime. The needle is placed through the middle of a wine cork. The cork is placed over the dime. When the needle is whacked with a hammer, the cork prevents it from bending so that the needle is forced to penetrate the dime.
As a preteen, I thought this was the coolest thing I had ever seen. I was going to try it myself! I got a cork, a needle, and a dime and went to the garage to get a hammer from Dad’s tool chest. I pushed the needle into the cork and placed the dime on the concrete floor and the cork on the dime. I knew from watching Mr. Wizard that I would need to hit the cork hard. So I lifted the hammer over my head and brought it down as hard as I could.
I was not old enough to appreciate the trade-off between hammer speed and accuracy nor to recognize the stupidity of holding the cork between my left thumb and index finger. The hammer missed the cork and came down squarely on my left thumb, which flattened out to the size of a half-dollar. I ran screaming from the garage into the house. Mom took one look and drove me to Marymount Hospital where I received two stitches. To date, I have never completed the needle and cork experiment. But the incident had a significant impact on my life because the tip of my left thumb is still numb.

When I visit high schools with my friend and colleague Dr. Charles Baylis (above), we are accompanied by a graduate student and Charlie’s vector network analyzer. Just the name, vector network analyzer, can sound boring to a high school student, so we pique interest with a bit of sizzle. Charlie asks for a volunteer to bring a cell phone up front. The vector analyzer shows a frequency sweep on a display. When the student calls a friend in class on the phone, the cell phone’s signal causes a distinct spike in the display, at the operating frequency of the cell phone. Much to the students’ delight, the frequency of the cell phone is identified. And the sizzle has been served! We are now able to talk about frequency, AM and FM radio, wireless frequency bands and the frequencies at which radar works.
The antenna Charlie uses is a cardboard tube from a roll of paper towels around which is wrapped a length of wire twisted into a helix. Although the do-it-yourself antenna captures the student’s attention, seeing their cell phones on the display is the sizzle that makes the technical topic more interesting.
When I teach a course, I too like to sell the sizzle at the beginning of each lecture. For a graduate course in information theory I teach, the students are told that they will learn why their cell phones use recently discovered coding that pushes the boundaries of what is mathematically possible in communication speed. I also tell them that we will prove that some things exist that we can also prove are unknowable. And there are numbers that a computer can’t compute. There also exists a single number, Chaitin’s number, that we know lies between zero and one. If we knew Chaitin’s number to finite precision, we could prove or disprove numerous open problems in mathematics. Large monetary awards await anyone who supplies a proof.
But guess what? Even though we know that Chaitin’s number exists, we can also prove it is unknowable. How’s that for sizzle? Contra-nerds may be bored. STEM nerds will drool with anticipation. I am convinced sizzle can be identified for every STEM class. I teach a number-crunching class on multidimensional signal processing where we talk of iterative algorithms converging to a fixed point. Sounds pretty boring huh? But consider the following sizzling example, understandable to all:
Take any number, say 559. Spell it out.
FIVE FIVE NINE
There are 12 letters. Spell TWELVE.
That’s 6 letters and that’s spelled
SIX
Six has 3 letters.
THREE
Three has 5 letters.
FIVE
Five has 4 letters.
FOUR
Four has 4 letters.
Four has 4 letters? Wait a minute. If we continue with this series, we will be saying “FOUR has 4 letters” indefinitely. We can’t go anywhere else from here.
There is a name for this situation. Four is said to be the fixed point of the iteration because FOUR is idempotent to the letter counting operation, which is to say that the same number occurs if you apply the operation once, twice, or 10 times.
Locking your car using the remote on your keychain is an example of an idempotent operation because locking your car once is the same as sequentially locking it two or even 10 times in a row. What’s fascinating is that, no matter what number you start with in the letter-counting exercise, you will converge to FOUR. The algorithm appears to have a universal basin of attraction and looks to be stable. STEM nerds typically find this algorithm fascinating and want to know more. Sizzle leads to more advanced discussions later.
My wife Monika is a contra-nerd. I told her about this letter-counting algorithm and convinced her, by forcing several examples on her attention, that the sequence always converges to FOUR. As one who gets enthusiastic about sizzle, I bubbled “Isn’t that fascinating? Isn’t that incredible?!” Monika shrugged her shoulders and, as a segue to initiating a new, non-nerd topic, unenthusiastically replied “Sure. I guess so.” Nerd sizzle only resonates with nerds.
My own career is full of mountains climbed to experience the sizzle on the other side. I remember being blown away by holograms and their ability to capture three-dimensional pictures on a two-dimensional surface. Today I know the beautiful theory behind the Nobel Prize-winning invention of holography. It was a big part of my Ph.D. dissertation. I’ve taught holography at the university level and even have a handful of publications on the topic. 1
Tomography, like magnetic resonance imaging (MRI), produces 3D images of your insides without cutting you up. Fascinated, I learned all I could and subsequently published a few papers on the topic.2 The fundamentals of CATscan tomography is a section in my book on Fourier analysis.3 And, despite writing scholarly books about tomography, I still find it mind-blowing. I was also powerfully drawn to the sizzle of neural networks, computers that work the way the brain works. I am fortunate to have been able to publish on neural networks in many periodicals4 and have even co-written a book on them.5
My latest sizzle is the theory of computation, which can be used to ask whether the human mind is functionally a computer or something beyond that. Can a computer truly be creative? Can we prove that things exist that are unknowable? This is astonishing mathematics to study.
Whether you are a nerd or a contra-nerd, it’s fun to identify your own sizzle to motivate your own mountain climbing. Fundamentally, mathematics inexplicably models reality and, for some, this is an attractive sizzle. Although finance majors typically aren’t usually considered STEM students, their mathematics can be very advanced. Ito Calculus is used to solve the stochastic differential equations needed to arrive at the Nobel Prize-winning Black-Scholes model for option pricing. (Even if you don’t know what this means, you must admit that the description itself is impressive.)
Recently, when I asked finance major Ryan Crews what his sizzle in finance was, he said it was the applicability of math to modeling reality. Those who don’t appreciate what Nobel Laureate Eugene Wigner called “The unreasonable effectiveness of mathematics in the natural sciences”6 are numbed by its everyday familiarity. Bell Labs scientist extraordinaire Richard Hamming expressed his astonishment at the profound effectiveness of simple counting numbers. Can you relate to this? :
I have tried, with little success, to get some of my friends to understand my amazement that the abstraction of integers for counting is both possible and useful. Is it not remarkable that 6 sheep plus 7 sheep make 13 sheep; that 6 stones plus 7 stones make 13 stones? Is it not a miracle that the universe is so constructed that such a simple abstraction as a number is possible? To me, this is one of the strongest examples of the unreasonable effectiveness of mathematics. Indeed, I find it both strange and unexplainable.7
Here is a simple example of the unreasonable effectiveness of mathematics at modeling reality. Consider the parabola given by the lowly equation “y is equal to a times x 2 “: y = ax2.
If the constant a is negative, the parabola is a bump. If positive, the parabola is a bowl. Here are three unrelated places where parabolas are modeled in nature:
First, if a baseball is hit in the air, its trajectory will follow a simple parabola8:
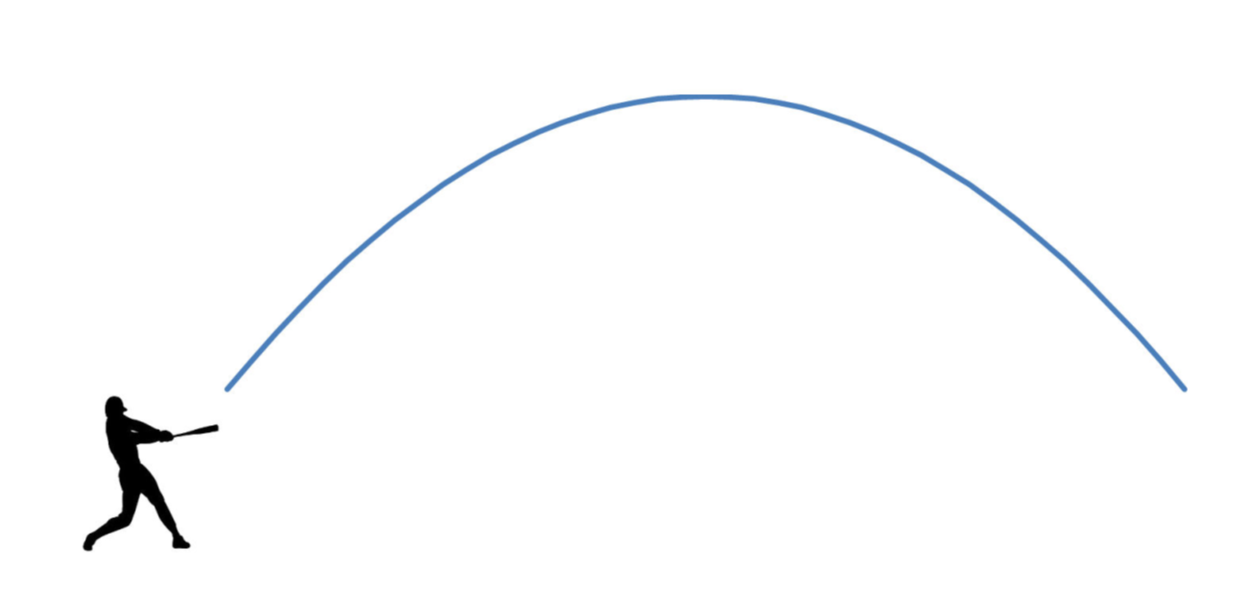
Second, the light pattern on the wall emanating from a nearby lampshade can make a parabola:
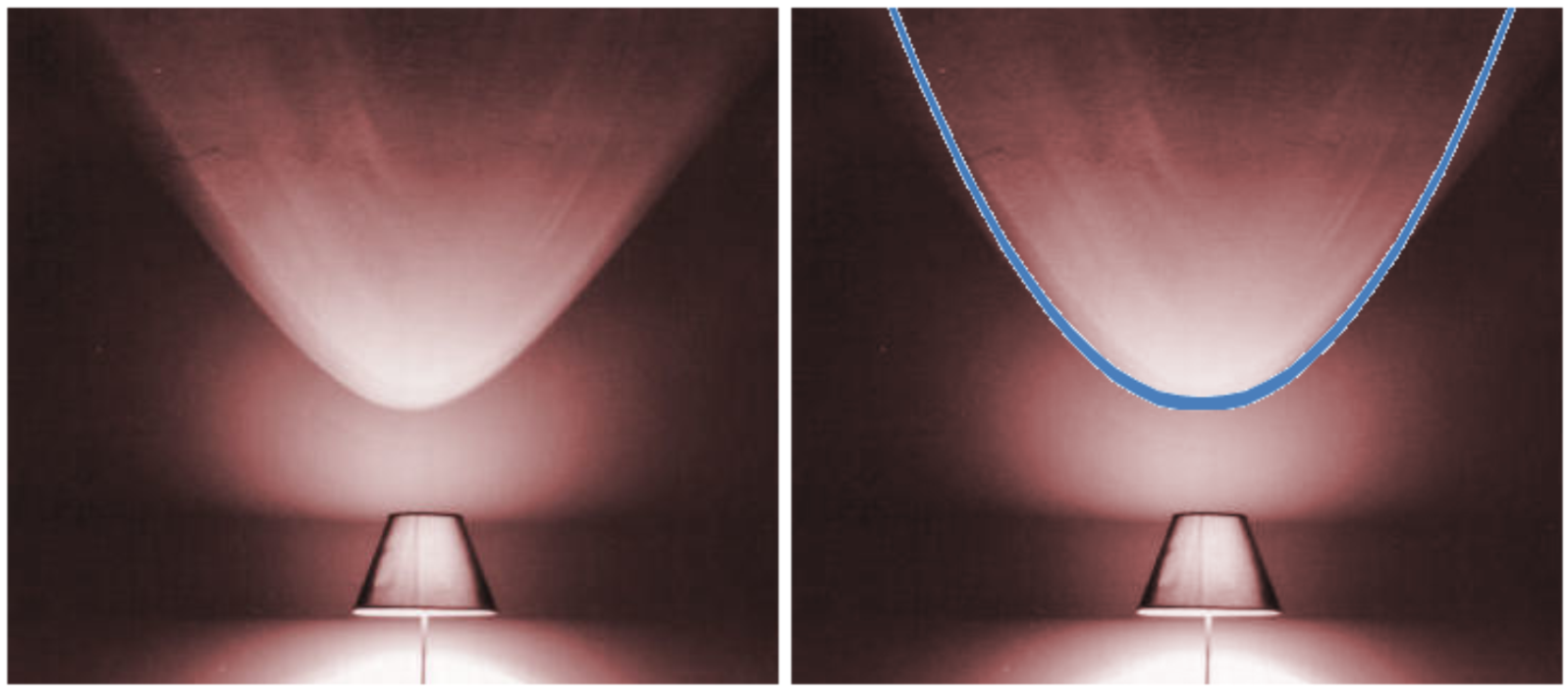
Students of analytic geometry will recognize this as a visual example of a conic section.
Third, even the curve of a banana can be modeled using a parabola.

Parabolas are everywhere. I find this to be both incredible and inexplicable.
Why is mathematics so effective in describing reality? The question is not a scientific one. It arises from philosophy and, like many questions from philosophy, is definitively unanswerable. This unattainable sizzle is a motivation in the minds of great thinkers like Wigner, Hamming, and finance student Ryan.
Following the allure of sizzle is fun. Many STEM nerd professions, such as research professorships, allow considerable freedom in the pursuit of interesting new ideas. I am blessed in this regard. In my experience, true STEM nerds are always pursuing some type of sizzle even in their spare time. Generally, the higher the academic degree, the greater the freedom STEM nerds have to pursue their sizzle of choice. And the pay is decent. So, if you love the pursuit of nerd sizzle, get a Ph.D.
Notes
1 R.J. Marks II, J.F. Walkup, and M.O. Hagler Volume hologram representation of space-variant systems, in Applications of Holography and Optical Data Processing edited by E. Marom, A.A. Friesem and E. Wiener-Aunear, Oxford: Pergamon Press, pp.105-113 (1977). T.F. Krile, R.J. Marks II, J.F. Walkup, and M.O. Hagler, Holographic representations of space-variant systems using phase-coded reference beams,Applied Optics, vol.16, pp.3131-3135 (1977). R.J. Marks II, Two-dimensional coherent space-variant processing using temporal holography,Applied Optics, vol. 18, pp.3670-3674
2 They are listed here.
3 Marks II, Robert J., Handbook of Fourier analysis & its applications, Oxford University Press, 2009
4 They are listed here.
5 Reed, Russell, and Robert J. Marks II. Neural smithing: supervised learning in feedforward artificial neural networks. MIT Press, 1999.
6 Wigner, Eugene P. “The unreasonable effectiveness of mathematics in the natural sciences. Richard Courant lecture in mathematical sciences delivered at New York University, May 11, 1959.” Communications on pure and applied mathematics 13, no. 1 (1960): 1-14. Text: The Unreasonable Effectiveness of Mathematics in the Natural Sciences
7 Richard Hamming, The Unreasonable Effectiveness of Mathematics,The American Mathematical Monthly, Vol. 87, No. 2, February 1980.
8 The parabolic path of the baseball is a first-order approximation. Other factors, including the baseball spin, humidity, and wind, must be considered in a real-life situation.
Related
The previous articles in this series:
- STEM EDUCATION 1. STEM Education 1. Pursuing Nerd Quality Over Nerd Quantity
- STEM EDUCATION 2. Stem Education 2. Not Everyone is Lucky Enough to Be A Nerd
- STEM EDUCATION 3. Killing People and Breaking Things Modern history suggests that military superiority driven by technology can be a key factor in deterring aggression and preventing mass fatalities
- STEM Education 4. Do STEM Nerds Need to Learn Latin? Well-roundedness is appropriate in applied STEM curricula to the extent that it rounds out the skills necessary for success as a STEM professional.
- Stem Education 5: What difference do family and privilege make to success? Robert J. Marks: A strong family helps a STEM nerd succeed. However, a “strong family” is not necessarily a family that had an easy ride, as my own story shows.
- STEM Education 6: How to Guide a Nerd Robert J. Marks: Students whose high school curricula are flexible can more easily develop and follow their God-given talents
Also by Robert Marks …
- Autonomous AI in War: Trial by Ordeal The more complicated a system becomes, the more difficult it is to analyze all of its actions.
- Top Ten AI hypes of 2018
