Some Infinities Are Bigger Than Others But There’s No Biggest One
Georg Cantor came up with an ingenious proof that infinities can differ in size even though both remain infiniteWhen a child is asked “what is bigger than infinity,” the response is often “Infinity plus one.”
No. Infinity plus one is still infinity.
But we can show that the number of points on the interval zero to one is a bigger infinity than the counting numbers are. The first clue is the fact that we can’t count the number of points on a line interval.
Try labeling the points on a line as points 1, 2, 3, etc. No matter what scheme you come up with, there will always be some points on the line segment that are not included in your count.
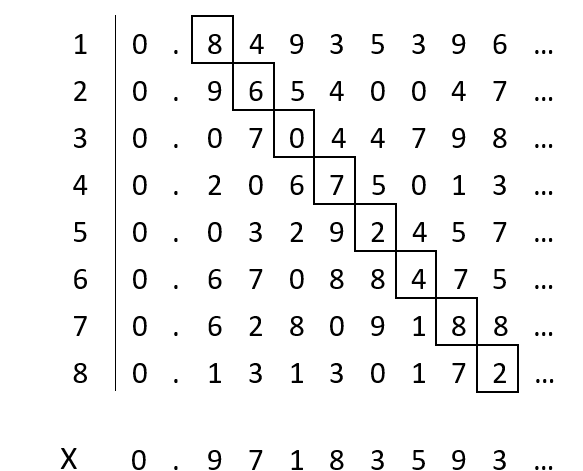
Georg Cantor (1845–1918) came up with an ingenious argument to show that the infinite number of points on a line was greater than the number of counting numbers. His method, called diagonalization, is illustrated in the figure shown:
Recall that the infinities of two sets are the same if there is a one to one correspondence between the two sets. The number of even numbers and the number of primes were both shown to be the same set size as the set of counting numbers. There is a one-to-one correspondence between the two sets.
If the points on a line were the same infinite size as the set of counting numbers, then we should find such a one-to-one correspondence. This is what the table shown attempts. The number 0.84935296… is being assigned to the first counting number 1. Remember, this point on the line is irrational and can go on forever. For the counting number 2, we assign the point 0.96540047… The table goes on and assigns a different number on the line interval to every counting number. Can there be a one-to-one correspondence?
No.
Look at the number X at the bottom of the table. This number does not appear on the list. The first digit in X, an 8, cannot be the first number on the list whose first digit is 9. It can’t be the second number on the list either. The second number has the number 6 as its second digit and the second number in X is a 7. The same applies to the number assigned to the counting number 3. Its third digit is a 0 and the third digit in X is a 1. On and on we go. The number X can’t be the fourth number, the fifth, and on and on to infinity. The number X is not on the list of numbers.
So the number of points on a line segment is greater than the number of counting numbers. It is a bigger infinity.
Cantor called the countable infinite, the infinity of all counting numbers, ℵ0. ℵ is the Hebrew letter aleph. The number of points on a line segment, a bigger infinity, is denoted by ℵ1. We are immediately prompted to ask if there is an even bigger infinity? The answer is yes. ℵ2 can be thought of as all of the set of points, squiggles, clumps of points, and combinations thereof that can be written in a square.

2022) by Robert J. Marks is available here.)
Cantor showed that a bigger infinity can always be constructed by taking the set of all subsets of a lower infinity. In general, there are 2M subsets of a set with M elements. If there are 3 elements in a set, there should be 23 =2×2×2=8 subsets. The eight subsets are A, B, C, AB, AC, BC, ABC and the null set. So a higher infinity than ℵn is the set of all subsets of ℵn . ℵn+1 is equal to 2 raised to the power of ℵn.
So there is no biggest infinity! A larger infinity can always be constructed.
Interestingly, I know of no one who can visualize ℵ3 and beyond. We have the math, but what does it mean? An analogy is our perception of 3 spatial dimensions. If I stretch my mind, I can visualize 4 spatial dimensions. But outside of a mathematical description, I cannot grasp the physical interpretation of 5 or more spatial dimensions.
We started off Part 1 of this series on infinities with an example of the lowly shepherd who resorted to stone counting to keep track of his sheep. Counting beyond 4 or 5 was simply beyond the shepherd’s ability so he gathered stones to make a one-to-one correspondence. We might scoff, but here we are seen to have similar limitations. Like the shepherd, we must resort to math ideas to deal with infinities above ℵ2 and spatial dimensions above 4. This is beyond our limited ability. But not beyond God’s. No wonder Georg Cantor sought an audience with Pope Leo XIII to discuss the theological implications of his theory of the infinite.
So ends our discussion of the infinite. It is a beautiful theory but infinity does not exist in reality. If it did, we’d have a lot of ludicrous and counterintuitive consequences to deal with.
We hope you enjoy this series on the unique, reality-defying nature of mathematical infinities. Here are all five parts — and a bonus:
Part 1: Why infinity does not exist in reality. A few examples will show the absurd results that come from assuming that infinity exists in the world around us as it does in math. In a series of five posts, I explain the difference between what infinity means — and doesn’t mean — as a concept.
Part 2. Infinity illustrates that the universe has a beginning. The logical consequences of a literally infinite past are absurd, as a simple illustration will show. The absurdities that an infinite past time would create, while not a definitive mathematical proof, are solid evidence that our universe had a beginning.

Part 3. In infinity, lines and squares have an equal number of points Robert J. Marks: We can demonstrate this fact with simple diagram. This counterintuitive result, driven by Cantor’s theory of infinities is strange. Nevertheless, it is a valid property of the infinite.
Part 4. How almost any numbers can encode the Library of Congress. Robert J. Marks: That’s a weird, counterintuitive — but quite real — consequence of the concept of infinity in math. Math: Almost every number between zero and one, randomly chosen by coin flipping, will at some point contain the binary encoding of the Library of Congress.
and
Part 5: Some infinities are bigger than others but there’s no biggest one Georg Cantor came up with an ingenious proof that infinities can differ in size even though both remain infinite. In this short five-part series, we show that infinity is a beautiful — and provable — theory in math that can’t exist in reality without ludicrous consequences.
You may also wish to read: Yes, you can manipulate infinity in math. The hyperreals are bigger (and smaller) than your average number — and better! (Jonathan Bartlett)
