Due to increased crowding of the radio spectrum, regulators have
begun practicing dynamic spectrum allocation in many bands. To allow the
dynamic allocation of spectrum to be performed over a larger portion of
the radio spectrum, transmitter and receiver amplifier circuitry must
be adaptable in real-time to meet changing operating frequency and
output spectrum requirements, while being power efficient and
maintaining acceptable bit-error rate (communications) and ambiguity
function (radar) properties. In most cases, a spectral mask is assigned
to a radar or communication transmitter output by regulators. In future
protocols supporting dynamic frequency allocation, this mask may be
adjustable based upon geographic and spectral proximities of nearby
wireless applications.
Adaptive impedance matching is needed to facilitate changes in operating frequency and spectral output.
Lu and Vaka-Heikkila have presented a micro-electrical mechanical
systems (MEMS) switching scheme to construct amplifiers with adaptive
output matching networks [1], [2]. For many applications, frequency-agile circuits must be tunable over a broad range. An adaptive impedance tuner is presented by Deve, who demonstrates tuning from 1 to 3 GHz [3]. Sun discusses the criticality of minimizing the number of iterations in impedance tuning algorithms [4]. Real-time impedance matching is demonstrated in the literature [5], [6], and Qiao demonstrates a tunable amplifier using a genetic algorithm for low-power communication applications [7]. Baylis discusses the criticality of reconfigurable transmitter power amplifiers for “solving the spectrum crisis” [8].
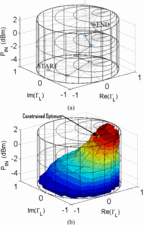
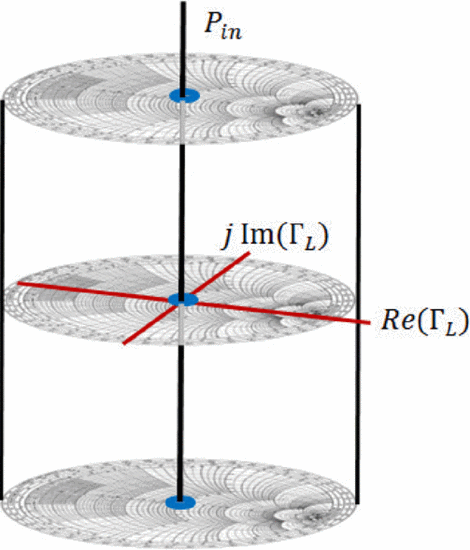
For visualization of multi-parameter circuit optimizations, the Smith
Tube has been introduced as an extension of the Smith Chart [9] [10] [11] [12] [13]. The vertical axis can represent input power [11], bias voltage [13], or bandwidth [9].
This paper overviews our recent contributions in fast circuit
optimizations for multiple and conflicting system objectives that will
be useful in the real-time, spectrum-aware optimization of communication
and radar transmitters.
SECTION II
VECTOR-BASED OPTIMIZATION IN THE SMITH CHART FOR MULTIPLE OBJECTIVES
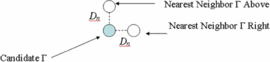
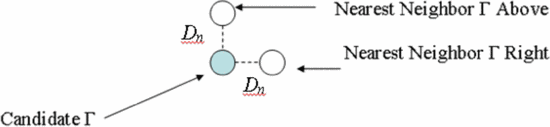
A vector-based algorithm for constrained optimization has been created in the Smith Chart. The load reflection coefficient 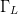 $\Gamma_{L}$
can be tuned in a real-time search to maximize the power-added
efficiency (PAE) while maintaining the adjacent-channel power ratio
(ACPR) below a pre-specified limit [14]. The
search vector is based on estimation of the PAE and ACPR gradients in
the Smith Chart from surrounding-point measurements separated by
neighboring-point distance
$\Gamma_{L}$
can be tuned in a real-time search to maximize the power-added
efficiency (PAE) while maintaining the adjacent-channel power ratio
(ACPR) below a pre-specified limit [14]. The
search vector is based on estimation of the PAE and ACPR gradients in
the Smith Chart from surrounding-point measurements separated by
neighboring-point distance 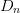 $D_{n}$, as shown in Fig. 1.
$D_{n}$, as shown in Fig. 1.
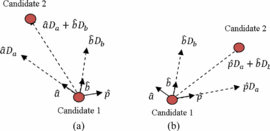
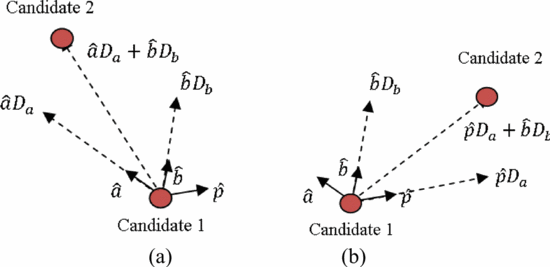
Figure 2 shows the construction of a search vector based on the gradient vectors to locate the next candidate 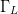 $\Gamma_{L}$ in the Smith Chart. Unit vectors
$\Gamma_{L}$ in the Smith Chart. Unit vectors 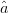 $\hat{a}$ and
$\hat{a}$ and 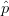 $\hat{p}$ represent the optimum ACPR and PAE directions, respectively, and are calculated from the gradients.
$\hat{p}$ represent the optimum ACPR and PAE directions, respectively, and are calculated from the gradients. 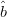 $\hat{b}$
is the bisector between these vectors. If the ACPR value at Candidate 1
is out of compliance, the search vector is constructed as follows:
$\hat{b}$
is the bisector between these vectors. If the ACPR value at Candidate 1
is out of compliance, the search vector is constructed as follows: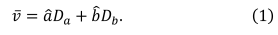 TeX Source\begin{equation*}
\bar{\nu}=\hat{a}D_{a}+\hat{b}D_{b}.
\tag{1}
\end{equation*}
TeX Source\begin{equation*}
\bar{\nu}=\hat{a}D_{a}+\hat{b}D_{b}.
\tag{1}
\end{equation*}
If the ACPR value at Candidate 1 is within compliance, the search vector is given as follows: TeX Source\begin{equation*}
\bar{v}=\hat{p}D_{a}+\hat{b}D_{b}.
\tag{2}
\end{equation*}
TeX Source\begin{equation*}
\bar{v}=\hat{p}D_{a}+\hat{b}D_{b}.
\tag{2}
\end{equation*}
The strengths of the vector components are given [14] by 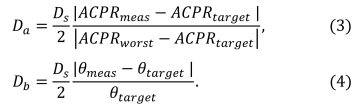 TeX Source\begin{align*}
& D_{a}=\frac{D_{s}}{2}\frac{\vert ACPR_{meas}-ACPR_{target}\vert}{\vert ACPR_{worst}-ACPR_{target}\vert},\tag{3}\\
& D_{b}=\frac{D_{s}}{2}\frac{\vert\theta_{meas}-\theta_{target}\vert}{\theta_{target}}.\tag{4}
\end{align*}
TeX Source\begin{align*}
& D_{a}=\frac{D_{s}}{2}\frac{\vert ACPR_{meas}-ACPR_{target}\vert}{\vert ACPR_{worst}-ACPR_{target}\vert},\tag{3}\\
& D_{b}=\frac{D_{s}}{2}\frac{\vert\theta_{meas}-\theta_{target}\vert}{\theta_{target}}.\tag{4}
\end{align*}
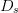 $D_{s}$ is the search-distance parameter selected by the user. The measured, goal, and worst-case values of ACPR and
$D_{s}$ is the search-distance parameter selected by the user. The measured, goal, and worst-case values of ACPR and 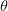 $\theta$,
the angle between the PAE and ACPR-PAE bisector vectors, are used to
calculate the search vector components. Measurement testing of the
algorithm was performed using a Maury Microwave Automated Tuner System
(ATS) load-pull setup with signal generator, power meter/sensor, and
spectrum analyzer from Keysight Technologies with chirp waveform
excitation. The device under test was a Skyworks packaged amplifier,
with the optimization goal to maximize PAE while maintaining ACPR
$\theta$,
the angle between the PAE and ACPR-PAE bisector vectors, are used to
calculate the search vector components. Measurement testing of the
algorithm was performed using a Maury Microwave Automated Tuner System
(ATS) load-pull setup with signal generator, power meter/sensor, and
spectrum analyzer from Keysight Technologies with chirp waveform
excitation. The device under test was a Skyworks packaged amplifier,
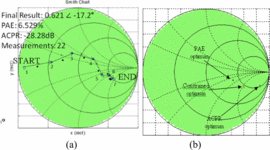
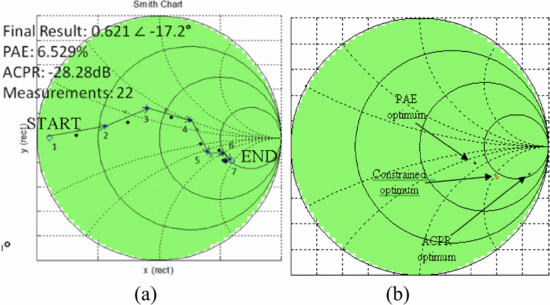
with the optimization goal to maximize PAE while maintaining ACPR 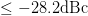 $\leq-28.2\mathrm{dBc}$. Figure 3
shows that the fast search algorithm measurement results compare very
well with the results extracted from traditionally measured load-pull
data. These results and algorithm test results
from other starting points show that between 11 and 25 measured points
were necessary to locate the constrained optimum in five searches
started from varying locations on the Smith Chart [14].
$\leq-28.2\mathrm{dBc}$. Figure 3
shows that the fast search algorithm measurement results compare very
well with the results extracted from traditionally measured load-pull
data. These results and algorithm test results
from other starting points show that between 11 and 25 measured points
were necessary to locate the constrained optimum in five searches
started from varying locations on the Smith Chart [14].
An expanded algorithm has been constructed
that has shown success in optimizing PAE under constraints on both ACPR
and delivered power [15]. This dual-constraint
situation is applicable to most communication and radar applications,
because the transmitted power is very critical to receipt of the message
with necessary signal-to-noise ratio (communications) or successful
illumination of a target (radar).
SECTION III
MULTI-PARAMETER, MULTI-OBJECTIVE REAL-TIME CIRCUIT OPTIMIZATION ALGORITHMS
The Smith Chart provides an optimization space to search for the constrained optimum 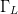 $\Gamma_{L}$.
If it is desired to optimize additional parameters simultaneously in
the real-time amplifier, additional dimensions are needed in the search
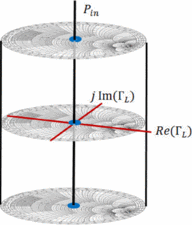
space. The Smith Tube (Fig. 4) allows visualization
for realtime optimization of multiple circuit parameters for multiple
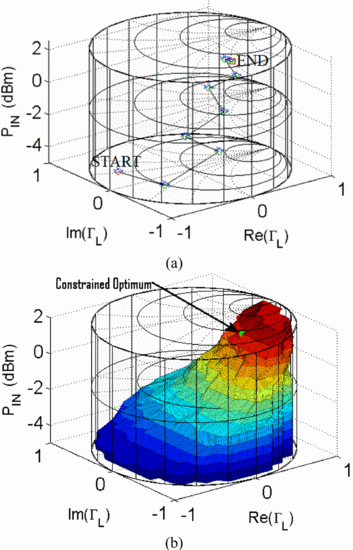
criteria. The vector-based search uses search vectors constructed as in Fig. 2, but in the three-dimensional search space, based on the three-dimensional gradient estimations. Figure 5 shows algorithm measurement results in the Power Smith Tube. In this measurement test, it was desired to optimize
$\Gamma_{L}$.
If it is desired to optimize additional parameters simultaneously in
the real-time amplifier, additional dimensions are needed in the search
space. The Smith Tube (Fig. 4) allows visualization
for realtime optimization of multiple circuit parameters for multiple
criteria. The vector-based search uses search vectors constructed as in Fig. 2, but in the three-dimensional search space, based on the three-dimensional gradient estimations. Figure 5 shows algorithm measurement results in the Power Smith Tube. In this measurement test, it was desired to optimize 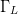 $\Gamma_{L}$ and
$\Gamma_{L}$ and 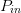 $P_{in}$ simultaneously to achieve the highest PAE possible while maintaining ACPR
$P_{in}$ simultaneously to achieve the highest PAE possible while maintaining ACPR 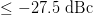 $\leq-27.5\ \mathrm{dBc}$ [12]. The constrained optimum was achieved in just 39 measurements for the three-dimensional search. A comparison of optimization from multiple starting
$\leq-27.5\ \mathrm{dBc}$ [12]. The constrained optimum was achieved in just 39 measurements for the three-dimensional search. A comparison of optimization from multiple starting 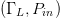 $(\Gamma_{L},P_{in})$ starting combinations is detailed in [12]. Measurement results varied from 24 to 39 experimental queries over five different tested starting points. Figure 5
shows that the endpoint from the intelligent search is very close to
the constrained optimum value assessed from multiple-power load-pull
data.
$(\Gamma_{L},P_{in})$ starting combinations is detailed in [12]. Measurement results varied from 24 to 39 experimental queries over five different tested starting points. Figure 5
shows that the endpoint from the intelligent search is very close to
the constrained optimum value assessed from multiple-power load-pull
data.
The Bias Smith Tube offers promise for simultaneous optimization of a device bias voltage with 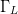 $\Gamma_{L}$ [13]. Efforts are underway to demonstrate a fast search algorithm for the optimum in the Bias Smith Tube.
$\Gamma_{L}$ [13]. Efforts are underway to demonstrate a fast search algorithm for the optimum in the Bias Smith Tube.
Multidimensional Smith Tubes and multi-parameter fast searches are being explored for real-time amplifier optimization [16].
As searches expand to greater dimensions, it will be necessary to
minimize the curse of dimensionality on the search convergence speed.
We have recently initialized a study comparing pattern, gradient, and
simplex searches in two, three, four, and five dimensional searches
using the Smith Tube framework [17].
Real-time circuit optimization searches for frequency-agile circuits
will be useful in designing spectrum-aware, reconfigurable communication
and radar transmitters. Fast circuit optimization algorithms will allow
transmitters to change operating frequency, spectral output, and
communication or detection capability while preserving power efficiency.
The Smith Tube is a useful visualization tool for these optimizations,
and ongoing work is exploring the use of fast searches in
multidimensional Smith Tubes to simultaneously optimize multiple circuit
parameters.
Acknowledgments
This work has been funded by the National Science Foundation (Grant
No. ECCS-1343316). The authors wish to thank Keysight Technologies for
cost-free loan of the Advanced Design System software, and Modelithics
for donation of their model libraries.