The increased use of the radar spectrum for sharing with wireless communications is resulting in new, innovative techniques for reconfigurable radar transmission from a cognitive radar platform. A cognitive radar can sense, adapt, and respond to its environment [1]–[2][3]. Frequency agility has been demonstrated to maximize power-added efficiency (PAE) and spectral compliance using software-defined radio (SDR) control [4] with a 90-W evanescent-mode (EVA) cavity tuning technology demonstrated by Semnani [5]. This technology must be merged with real-time spectrum sharing and radar signal processing, as described by Kirk [6], and implemented in a system known as “SDRadar”. However, a major challenge of this merger is that the EVA cavity tuner can require over 100 ms to perform some tuning operations, whereas the coherent processing interval (CPI) of a radar is often on the order of a few milliseconds. As such, it is not possible to adjust the circuit configuration for every individual CPI. Instead, the average performance over multiple CPIs can be optimized. This paper describes how impedance tuning can successfully be merged with the metacognitive decision process of a spectrum sharing cognitive radar.
SECTION II.
Tuning Options
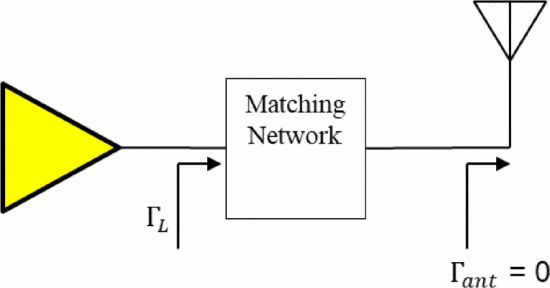
Upon deciding the transmit parameters (center frequency, bandwidth, waveform—collectively referred to as the SDRadar's “action” or “state”) in real time, the system will reconfigure a matching network to optimize the impedance shown to the power amplifier device. This concept is shown in Fig. 1. The impedance (and therefore the load reflection coefficient ΓL) will be optimized to deliver maximum power to the load device from the matching network. For these experiments we demonstrate matching assuming that a matched impedance is presented to the matching network by the next stage, possibly the antenna (i.e. Γant=0).
Dockendorf demonstrates a modified gradient search for a single operating frequency and bandwidth, where the search is performed in the two-variable space of n1 and n2, which are the position numbers of the resonator discs in the EVA cavity tuner [4]. More specifically, the method in [4] is useful for occasional (every 10–20 seconds) changes in operating frequency, the cognitive spectrum-sharing radio proposed by Kirk [6] is expected to change operating frequency and bandwidth as frequently as every CPI, which is expected to be potentially less than 10 ms. As the method of [4] requires a consistent system configuration throughout the optimization process in order to evaluate the effects of varying load impedance, whereas the tuning technology is unable to adjust on the time scale required, i.e., it is incompatible with the needs of a rapidly adapting system such as the SDRadar. To compensate for this, the gradient search method can be adjusted to utilize information from multiple observed transmit states during a single iteration; with the goal of maintaining the performance of the overall system across multiple states.
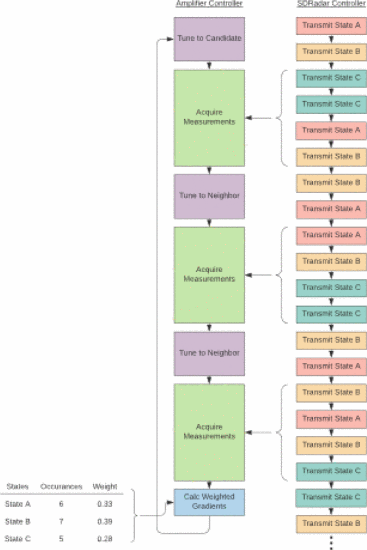
Rather than the modified gradient search of Dockendorf [4], which is a constrained maximization of PAE under spectral mask constraints, we modify the search into a simple gradient search to maximize the output power Pout at the output of the tuner. Fig. 2 shows a possible scenario where the transmit states are quickly changing relative to the tuning times. In this simplified scenario, three transmit states occur in random order, and it is desired that the selected tuner configuration minimizes the weighted distance to the optimum tuner configuration for each observed state. The left column represents the steps within a single iteration of the amplifier controller's algorithm, while the right column represents the sequence of states selected by the SDRadar controller. For gradient evaluation, the EVA tuner begins at the candidate point and then must tune to the two neighboring points in the (n1,n2) plane required to assess how the power delivered to the load varies with load impedance for each transmit state. At the end of the measurement window, consisting of N measurements, an estimate of the gradient of the delivered power is calculated for each transmit state. Each of these gradients are weighted according to the number of times each transmit state occurs at the candidate point and two neighboring points. In the bottom left of Fig. 2, the number of occurrences is shown for each transmit state, and the weight that each state's results is given in the final gradient calculation is shown.
Note that a state must be observed at each step of the current gradient iteration (the candidate and both of its two neighboring points) to be considered as a valid state; otherwise, a gradient estimate cannot be computed for that state. In situations where a state is only observed at some (but not all) of these steps, its performance during the current iteration is ignored, and the weights are computed as if the state were never transmitted.
The overall search vector is calculated as a weighted average of the gradients:
v¯=Σnwnv¯n,(1)
View Source \begin{equation*}
\bar{v}=\Sigma_{n}w_{n}\bar{v}_{n}, \tag{1}
\end{equation*} where wn is the weight calculated for state n based on the relative number of occurrences of that state in a given time frame and v¯n is a Pout gradient estimate for state n with respect to ΓL. For a total of N′ measurements corresponding to valid states, where state n was encountered cn times, the weights accompanying each vector v¯n are given by
\begin{equation*}
\bar{v}=\Sigma_{n}w_{n}\bar{v}_{n}, \tag{1}
\end{equation*} where wn is the weight calculated for state n based on the relative number of occurrences of that state in a given time frame and v¯n is a Pout gradient estimate for state n with respect to ΓL. For a total of N′ measurements corresponding to valid states, where state n was encountered cn times, the weights accompanying each vector v¯n are given by wn=cnN′.(2)
View Source \begin{equation*}
w_{n}=\frac{c_{n}}{N^{\prime}}. \tag{2}
\end{equation*}
\begin{equation*}
w_{n}=\frac{c_{n}}{N^{\prime}}. \tag{2}
\end{equation*}
The resulting step vector is then used in place of the gradient estimate of [9] to select the next candidate location in the (n1,n2) plane.
In a sense-and-respond situation where spectral prediction is not used, the approach of using past states during a given time period should be used to determine the weights (as illustrated in Fig. 2). In a predict-and-respond situation where spectral prediction is used, a schedule of future states to be transmitted should be available. The weights shown in the lower left of Fig. 2 could then be calculated based on the relative occurrences of each state in the future schedule. We will herein use past states to give the weighted average best tuner (n1,n2) setting.
SECTION III.
Experimental Results
The proposed algorithm was tested with a Microwave Technologies MWT-173 field-effect transistor (FET) with VDS=4.5V,VGS=−1.4V, and Pin=14 dBm. This transistor is driven by a dynamic transmission system that chooses between three different transmit states with equal probability. These states correspond to RF center frequencies of 3.1, 3.3, and 3.5 GHz. A new state is selected (with replacement) for each measurement performed during a run of the search algorithm. For the results of this section, a measurement window N=20 was used, meaning that at each tuner position visited by the search, 20 measurements were taken of randomly varying states prescribed by the system.
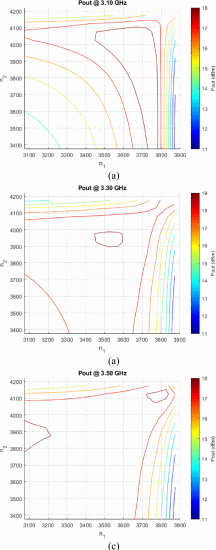
To allow comparison of algorithm results with traditionally measured data, Fig. 3 shows the output power contours for each individual state that was used. While these states have similar performance for high values of n1 and n2, they have different performance levels and contour slopes for most of the search space. For example, Pout drops significantly when moving to the bottom left of the (n1,n2) plane at 3.1 GHz, while remaining reasonably high for 3.3 and 3.5 GHz in the same region.
Three trials were performed for this search using random selection of measured states during the search from the three possible states. For the sake of simplicity, each state was given an equal weight in terms of state occurrence probability (despite the randomly varying occurrence of each state during the search.)
Fig. 4 shows the search path taken by three separate runs of the search starting from (n1,n2)=(3300,3600). The variations derive from both measurement noise, changes in the actual relative occurrences, and orders of occurrence of the three operating-frequency states. Despite taking different paths (directed by the varying distributions of observed states), all searches converge in the same region, as expected because each underlying probability distribution for the randomly generated states is the same.
Table I compares Pout at the endpoint for each individual frequency and the weighted average for each trial in Fig. 4. This data shows that even though the endpoint is not optimum for each frequency, the overall average performance is still good. The final column for average Pout does not necessarily equal the average of the Pout for the three frequencies since it is the weighted average of the measured powers based on the random distribution seen at the endpoint.
Fig. 5 shows the search paths taken by three separate runs, labeled as Trial 4, Trial 5, and Trial 6, that start at three different (n1,n2) locations. Trial 6 ends very close to the end of Trail 4 and thus the ‘X’ indicating it is obscured. The fact that all of these searches that start from different points in the search space still converge near the endpoints of Trials 1, 2, and 3 shown in Fig. 4 demonstrates robustness of the search.
Table II shows the Pout values at three frequencies at the endpoint for the searches with varied starting points (Trials 4, 5, and 6). This data reinforces the fact that while the search endpoint may not be optimal for each point, the average performance is good and demonstrates a good compromise in the tuning to provide good performance at all of the operating frequency states.
Fig. 6 shows the search path of Trial 5 with the gradient vectors shown for all three frequencies (3.1, 3.3, and 3.5 GHz) at each candidate (n1,n2) point. This provides a visual demonstration of how the gradient search vectors combine to create the search path. The gradients for each individual state are calculated independently and then normalized to have the same length. These steepest-ascent direction vectors of equal length are then multiplied by the weights of the corresponding state, and the vectors are combined to give the direction in which the search will proceed to the next candidate. This vector is then scaled to have magnitude equal to the current step size parameter setting in the gradient search. Near the start point, the gradients for the three states are oriented similarly. However, as the search gets to its third candidate, the 3.5 GHz gradient is oriented nearly opposite to the 3.1 GHz gradient, and significantly different from the 3.3 GHz gradient. As the endpoint is approached, the gradients remain oppositely directed, illustrating the tension between the different state gradients as the average position begins to converge. A weighted average of the emphasis on performance for the three states is expected based on the relative occurrences of the states during the gradient evaluations. This weighted performance is shown to be successful based on the results shown in Table II.
An algorithm designed to optimize transmitter power amplifier impedance tuning for average output power in a frequency-agile software-defined radar system has been demonstrated. The search is a demonstration of a fast, real-time impedance tuning procedure that can allow average output power and range performance to be optimized in a situation where the tuning operation is much slower than the change in operating frequency. Using an EVA cavity tuner with a tuning search time of 2–10 seconds, this approach can be utilized in systems with a much faster CPI. Next steps include the implementation of this search in a real-time software-defined radar platform in a continuous operating environment. In such a situation, it will be useful to assess the need for the performance of impedance tuning based on detection of the average states changing significantly. This investigation is planned as part of the ongoing collaborative Army Research Laboratory SDRadar effort.
ACKNOWLEDGMENT
The authors are grateful to John Clark of the Army Research Laboratory for his helpful insights in preparing this paper.
![]() \begin{equation*}
\bar{v}=\Sigma_{n}w_{n}\bar{v}_{n}, \tag{1}
\end{equation*}
\begin{equation*}
\bar{v}=\Sigma_{n}w_{n}\bar{v}_{n}, \tag{1}
\end{equation*}![]()