Introduction
Radar spectrum is becoming increasingly congested, and new techniques continue to emerge for dynamic radar spectrum sharing. Much of the S-band radar allocation in the United States continues to be reallocated, and the 3.45 to 3.7 GHz range is now shared between radar and wireless communications [1]. Cognitive radar systems [2]–[3][4] can assess and respond to their environment, and many cognitive radar systems can sense spectrum use and then adjust operating frequency, bandwidth, and the transmitted waveform to coexist with other wireless operations [3], [5]–[6][7][8][9]. An important part of cognitive radar transmission in spectrum sharing scenarios is the ability to optimize transmission range and efficiency after changing to a new operating frequency. If a tunable matching network is present, such adjustments can be performed in real-time.
It has been shown that power-amplifier output power and power-added efficiency (PAE) can be significantly enhanced by strategic design of load-impedance terminations at harmonic frequencies. Stancliff describes an approach to perform loadpull measurements using harmonic terminations, varying fundamental and harmonic load impedances to maximize the output power or efficiency of a nonlinear power amplifier [10]. Benedikt describes harmonic tuning using a 30 W active loadpull system, where a voltage wave is injected back toward the amplifier to emulate the waveform reflected from a given load impedance. The voltage and current waveforms can be viewed and engineered using an approach called “waveform engineering” to maximize power or efficiency [11]. Vadala describes the use of low-frequency current-voltage measurements to perform characterizations that allow harmonic terminations to be selected [12]. A back-and-forth method of fundamental and harmonic load- and source-pull measurements is demonstrated by Colantonio [13].
Real-time harmonic tuning techniques are useful because narrow-band, tunable matching networks are used rather than wideband, fixed matching networks. Bode [14] and Fano [15] have demonstrated that requiring higher bandwidth theoretically results in degrading the quality of the match [16]. If a network can be designed over a narrow band and adjusted in real-time when the operating frequency is changed to re-optimize performance, then better output power or efficiency at each frequency is likely to be obtained, leading to increased range of the radar and more efficient use of transmitter power supplies.
Harmonic Tuning Algorithm
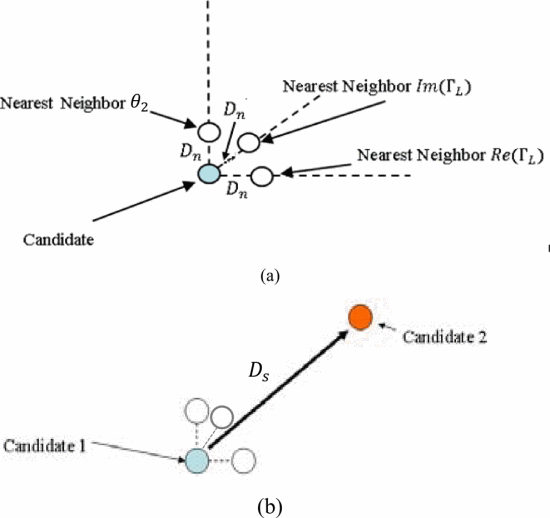
Fast simultaneous tuning of the fundamental and harmonic impedances (related to reflection coefficients) can be performed using the algorithm described in Fig. 1. Fig. 1 shows an illustration of the gradient search in three dimensions for simultaneous fundamental (
(a) Visualization of gradient estimation in three-dimensional search space. Neighboring points are used to assess the change in PAE in each dimensional direction, allowing estimation of the gradient. (b) Search step visualization in three-dimensional search. The search proceeds in the direction of the PAE gradient to the next candidate.
At the beginning of the gradient search, neighboring points are measured by varying each by the neighboring-point distance
The Smith Tube [17] is a useful tool for visualizing the search progression, and is a three-dimensional extension of the
Optimization Search Results
The algorithm was tested experimentally in simulations using Keysight Technologies' Advanced Design System (ADS) microwave circuit simulation software. A Modelithics model for the On Semi MMBFU310LT1 junction field-effect transistor model with
A. Traditional Harmonic Load-Pull Pre-Design
For comparison with search algorithm results, a traditional harmonic-tuning design approach was used, where fundamental load-pull measurements were first used to select
Fig. 3 shows the fundamental load-pull contours that describe the PAE variation over
The optimum PAE for fundamental impedance variation is 22.7% at
Traditional 500 MHz simulated fundamental load-pull contours with fixed open-circuit second- and third-harmonic terminations, showing optimum
Fig. 4 shows the second-harmonic load-pull contours with the fundamental reflection coefficient fixed to the previously determined fundamental optimum
Traditional 500 MHz simulated second-harmonic load-pull contours with fixed fundamental termination
The optimum third-harmonic termination was found to be
Traditional 500 MHz simulated third-harmonic load-pull contours with fixed fundamental termination
Traditional 500 MHz simulated fundamental load-pull contours with fixed
B. New Fast Gradient Search for Real-Time Reconfiguration in Frequency-Agile Radar Transmitters
Using the fast gradient search technique of Fig. 1, a search was performed in the four-dimensional space consisting of the four real search parameters
The search was performed to maximize PAE, and its trajectory is shown in Fig. 7. The search trajectory, as evidenced by Fig. 7(a) and Fig. 7(b), first shows a significant adjustment in the fundamental reflection coefficient (the plane of both Smith Tubes) and then shows a significant upward trajectory in the
Smith tubes describing the 500 MHz PAE optimization trajectory magnitude of fundamental load reflection coefficient with (a) Second-harmonic reflection-coefficient phase
Fig. 8 shows the progression of PAE and output power during the search of Fig. 7. Fig. 8(a) shows that PAE plateaus at approximately 23%, corresponding with the end of its trajectory parallel to the horizontal plane of the Smith Tube. This part of the search seems to result in a large change in the fundamental termination but negligible change to the second- and third-harmonic phase values. The green triangles in Fig. 8(a) indicate the measured points that represent the highest PAE values measured at or before their measurement numbers. Significant change in the trajectory of the search happens between measurements 25 and 30, and the second-harmonic termination phase begins to be adjusted, providing approximately 45% PAE, an increase of over 20% PAE from the results obtained in the first part of the search, where the primary adjustments were performed on the fundamental termination. In this search, very little adjustment of the third-harmonic reflection coefficient ended up occurring. Notably, the locations of the reflection-coefficient terminations resulting from the fast optimization search are similar to the traditional design results shown in Fig. 6, both in terms of Smith Chart location and maximum PAE achievable, as summarized in Table I. In addition, similar benefits were seen from performing second-harmonic tuning in addition to fundamental tuning.
(a) PAE and (b) Amplifier output power
To demonstrate the need for reconfiguration in changing frequencies, a second search was performed at a frequency of 300 MHz beginning at the fundamental and harmonic reflection coefficient values selected as the end point of the first search. Changing frequency while presenting the same reflection coefficients reduces the PAE by 30.0% to 17.3%. The search trajectory is displayed in Fig. 9, starting at the previous frequency's optimum, and shows that the optimum location moves significantly when changing frequency. The algorithm allows reconfiguration to obtain
Smith tubes describing the 300 MHz PAE optimization after frequency change trajectory magnitude of fundamental load reflection coefficient with (a) Second-harmonic reflection-coefficient phase
An additional search was performed at 500 MHz using the same device and bias settings. For this search, however, output power
(a) PAE and (b) Amplifier output power
Smith tubes describing the 500 MHz output-power optimization trajectory magnitude of fundamental load reflection coefficient with (a) Second-harmonic reflection-coefficient phase
Conclusions
A fast real-time search allowing simultaneous optimization of the fundamental and harmonic impedances in a radar transmitter power amplifier has been demonstrated in simulations. Gradient searches to optimize PAE or output power, which is related to radar range, have been demonstrated in the four-dimensional Smith Tube search space. The search results show significant improvement over only optimizing the fundamental reflection coefficient. Next steps include the development of a high-power harmonic tuning network and implementation of the algorithm in tuning this device.
ACKNOWLEDGMENTS
The authors are grateful to Modelithics for the donation of model libraries to Baylor University under the Modelithics University Program.


![Fig. 2. - The Smith tube [17] is a three-dimensional, cylindrical extension of the Smith chart, with the third axis representing an additional parameter. Here the third axis represents $\theta_{2}$, the phase of $\Gamma_{L, 2}$.](./2020-ReconRadar_files/153_4140-fig-2-source-small.gif)