Introduction
Multifunction arrays can provide spatial multiplexing to ease congestion on the radio spectrum. Radar and communication signals at the same frequency can be broadcast out of the same aperture, using direction as the discriminating parameter. In a coexistence scenario, the signal would likely be required to meet a spectral-spatial mask, an extension of the typical spectral mask into the spatial transmission domain [1]. Building a spatially multiplexed, multi-beam transmission aperture requires two basic considerations: (1) circuitry considerations allowing maximum transmitted signals in the desired directions while minimizing spurious beams in unwanted directions, and (2) design of the array element excitation currents to provide the desired waveforms in the desired directions. We overview these two considerations, along with some potential solutions to realize directional transmissions in a dual- or multi-beam radar-communication system.
McCormick discusses the concept of using a single aperture to simultaneously transmit radar and communication waveforms [2]. Daly presents a concept known as directional modulation for simultaneous communication transmission in multiple directions from phased arrays [3]. This concept is extended by Hamza and Amin into a radar system that employs sidelobe modulation for communication through the pattern spatial sidelobes [4].
While the canonical techniques are useful, challenges abound in implementation of a multi-beam transmitter array. Sandrin [5] and Larsson [6] describe how nonlinearities in the power amplifiers of the transmitter array elements cause undesired spurious beams. This “spatial intermodulation”, when combined with frequency intermodulation, can result in significant unwanted spatial and spectral content being undesirably broadcast from the transmitter array, as calculated by Hemmi [7] and described by Haupt [8].
This paper describes the use of array amplifier impedance tuning and directional modulation techniques to enable secure, agile multi-beam transmissions that can quickly optimize performance after changes in operating frequency and scan angle. This will enable sharing of precious spectral and spatial resources in real-time.
Scenario
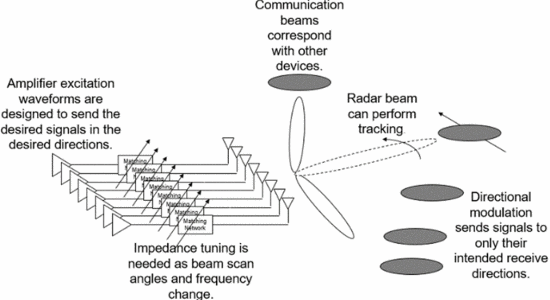
A typical scenario requiring directionally modulated, multi-beam transmission from a phased array is shown in Fig. 1.
Several innovations are needed to make the scenario of Fig. 1 a reality. First, the transmit array elements must be optimized to maximize range of the radar operations, provide adequate communication range, and reject unwanted spatial beams. Second, directional modulation must be contrived to allow successful transmissions of desired digital communication signals in the directions of the communication receivers, while providing a radar waveform that has the desired range/Doppler ambiguity characteristics.
Spurious-Free Multi-Beam Transmission
The literature describes different approaches for providing spurious-free multi-beam transmission. O'Connor and Rabideau present a signal processing approach to minimizing the unwanted spurious beams [9]. Pecarrelli overviews a menu of techniques that can be used to defeat nonlinearity-related spread in spatial transmissions [10]. Braithwaite demonstrates the use of predistortion to remove unwanted spatial artifacts in multi-beam transmission [11]. Dunn shows how predistortion can be applied in a situation where the antenna impedance changes based on a scanning array that changes direction (and hence changes the mutual coupling between the antenna elements) [12].
While predistortion can provide useful results through the apparent linearization of the transmission (whereas in actuality the system is not linearized; the transmit waveform is merely adjusted to compensate for the nonlinearity), transmission ranges of the different beams are also important, as are the gain and power-added efficiency of each of the element power amplifiers. Because the power amplifiers generally consume more supply power than any of the other elements in the transmitter chain, their amplifiers should be configured to transmit efficiently to maximize the entire system efficiency. Rodriguez-Garcia demonstrates the effectiveness of element-wise impedance tuning for single-beam transmission in a recent paper [13]. In this work, a four-element uniform linear patch array was used for transmission. The work makes use of a co-simulation platform in Keysight Technologies' Advanced Design System (ADS) and Momentum platforms. The antenna elements were designed using Rogers RO4003C substrate parameters and were configured for an operating frequency of 3.55 GHz. A Modelithics nonlinear model for the Microwave Technologies MWT-173 Gallium Arsenide (GaAs) metal-semiconductor field-effect transistor (MESFET) biased at Vcs == - 1.5 V and VDS== 4.5 V was used as the active device, with reconfigurable impedance matching networks designed by Calabrese [14] connected between the transistors and antennas. The simulation results were shown to yield radar range improvements of up to 26.5 percent from impedance tuning, depending on scan angle. It is also shown that impedance tuning can significantly and undesirably affect the array pattern if the same tuning settings are not used in all of the elements [13]. This underscores the need to ensure that the magnitude and phase modifications are similar in all elements following impedance tuning operations. Fig. 2(a) shows the array pattern for a simulation test without application of impedance tuning, Fig. 2(b) shows the array pattern with impedance tuning where all element tuners are tuned identically, and Fig. 2(c) shows the much different array pattern that results when the impedance tuners are set to different settings that still yield similar reflection coefficients (reprinted from [13]). If the impedance tuners affect the magnitudes or phases of the transmitted waveform differently, then the array pattern will not appear as desired.
Rodriguez-Garcia also demonstrates that use of reconfigurable matching circuits at the power amplifier outputs in the array can improve the transmission pattern and amplifier element gain values within a transmit array in a case of dual-beam transmission, such as radar and communications using the same aperture [15]. This addresses both the linearity and efficiency of the transmitter. This demonstration points toward impedance tuning as a potential solution to optimize for both linearity and efficiency in real-time.
Directional Modulation
Whereas transmitter techniques can be used to provide clean beam directions and transmitter strengths in the desired directions, directional modulation must be used to ensure that the desired messages reach only their intended directions. A form of directional modulation is required if more than one simultaneous message is to be sent across the different transmission directions. Fig. 3 shows an example of directional modulation.
Xie
describes directional modulation approach with an equation allowing
matrix inversion to directly solve for the phasor excitation currents of
the array elements [16]. The matrix equation is formulated as follows:
\begin{equation*}\mathbf{r}=\mathbf{H}(\Theta)^{\mathrm{H}}\mathbf{w}\tag{1}\end{equation*}
\begin{equation*}\boldsymbol{H}(\boldsymbol{\theta})=\frac{1}{\sqrt{M}}\left[\begin{array}{cccc}
1
& 1 & & \ldots \\
e^{-j k d \cos \theta_{1}} & e^{-j k d \cos \theta_{2}} & \cdots
& e^{-j k d \cos \theta_{M}} \\
e^{-j 2 k d \cos \theta_{1}} & e^{-j 2 k d \cos \theta_{2}} &
\cdots & e^{-j 2 k d \cos \theta_{M}} \\\vdots & \vdots &
\vdots & \vdots \\
e^{-j(N-1) k d \cos \theta_{1}} & e^{-j(N-1) k d \cos \theta_{2}}
& \cdots & e^{-j(N-1) k d \cos
\theta_{M}}\end{array}\right]\tag{2}\end{equation*}
Directional modulation provides directional transmissions, with the capability of obscuring the transmitted messages in other designated directions.
The \begin{equation*}\left[\begin{array}{c}
r_{1}
\\
r_{2} \\\vdots \\
r_{M}\end{array}\right]=\frac{1}{\sqrt{M}}\left[\begin{array}{cccc}
1 & e^{j k d \cos \theta_{1}} & \cdots & e^{j(N-1) k d \cos
\theta_{1}} \\
1 & e^{j k d \cos \theta_{2}} & \cdots & e^{j(N-1) k d \cos
\theta_{2}} \\
1 & e^{j k d \cos \theta_{3}} & \cdots & e^{j(N-1) k d \cos
\theta_{3}} \\\vdots & \vdots & \vdots & \vdots \\
1 & e^{j k d \cos \theta_{M}} & \cdots & e^{j(N-1) k d \cos
\theta_{M}}\end{array}\right]\left[\begin{array}{c}
w_{1} \\
w_{2} \\\vdots \\
w_{n}\end{array}\right]\tag{3a}\end{equation*}
\begin{equation*}\left[\begin{array}{c}
r_{1}
\\
r_{2} \\\vdots \\
r_{M}\end{array}\right]=\frac{1}{\sqrt{M}}\left[\begin{array}{c}
w_{1}+w_{2} e^{j k d \cos \theta_{1}}+w_{3} e^{j 2 k d \cos
\theta_{1}}+\cdots+w_{N} e^{j(N-1) k d \cos \theta_{1}} \\
w_{1}+w_{2} e^{j k d \cos \theta_{2}}+w_{3} e^{j 2 k d \cos
\theta_{2}}+\cdots+w_{N} e^{j(N-1) k d \cos \theta_{2}} \\\vdots \\
w_{1}+w_{2} e^{j k d \cos \theta_{M}}+w_{3} e^{j 2 k d \cos
\theta_{M}}+\cdots+w_{N} e^{j(N-1) k d \cos
\theta_{M}}\end{array}\right]\tag{3b}\end{equation*}
The goal of the problem is to solve for the array element excitation current phasors
To calculate the excitation phasors, both sides of (1) can be left-multiplied by the Moore-Penrose pseudoinverse of \begin{equation*}\left[\mathbf{H}(\boldsymbol{\theta})^{H}\right]^{\dagger}
\mathbf{r}=\left[\mathbf{H}(\boldsymbol{\theta})^{H}\right]^{\dagger}
\mathbf{H}(\boldsymbol{\theta})^{H} \mathbf{w}\tag{4}\end{equation*}
Simplifying gives a solution for the array excitation current phasors that need to be applied:
\begin{equation*}\mathbf{w}=\left[\mathbf{H}(\boldsymbol{\theta})^{H}\right]^{\dagger} \mathbf{r}\tag{5}\end{equation*}
The legitimate solution of (5) depends on the size of H(0)H, which is
If
M=N If
M<N If
M>N M
A simple MATLAB script was constructed to test the effectiveness of this basic method using the built-in pinv Moore-Penrose pseudoinverse function. Four test cases were constructed for the directional modulation approach, including two cases for which M < N and exact solutions are expected to result. Two of these test cases were constructed to examine the results of the approach when difficulties are expected: a situation in which two different messages were specified for the same angle, and a situation in which M > N (overdetermined system).
Simulations were performed using a 16-element linear array, with half-wavelength spacing. Four-bit digital messages were used using phase-shift keying with 16 symbols (16-PSK). Symbol indices were used to identify the bit combinations sequentially from 0000 to 1111. 0000 was assigned an index of value 1, and 1111 was assigned index 16. A symbol index was specified for transmission in each specific direction of each test case. The four test cases were specified as follows:
Test 1: 5 directions:
30∘,50∘,90∘,110∘,140∘; Test 2: 7 directions:
70∘,60∘,40∘,50∘,90∘,115∘,127∘; Test 3: 7 directions:
70∘,60∘,40∘,50∘,90∘,70∘,127∘; Test 4: 17 directions:
5∘,10∘,17∘,20∘,25∘,28∘,32∘,33∘,45∘,50∘,38∘,80∘,90∘,92∘,94∘,110∘,123∘;
Test 1 and Test 2 both provide a situation where the number of specified directions is fewer than the number of array elements, so an exact solution is expected, where the symbol indices calculated are actually received. Indeed, both Test 1 and Test 2 provided exact calculation of the symbols transmitted in different directions. This was validated using MATLAB. The received symbols are shown with the desired symbols in Fig. 4. The desired symbols are received based on the directional modulation approach using the Moore-Penrose pseudoinverse.
Test 3 provided a scenario in which two different symbols were both assigned for transmission in the
The Test 3 message specifications and calculated messages are shown in Fig. 5. As evidenced by the left column, the different message values
Test 4 is a scenario where a larger number of receiver directions
Hamza has also developed a response that, rather than calculating the excitation current weights directly using the pseudoinverse, uses three objectives that must be accomplished through optimization. This approach is found to reduce all sidelobe levels, while providing the opportunity for wide-beam radar over a range of directions, and is thoroughly described, along with a presentation of results, in [4].
Combining Array Impedance Tuning and Directional Modulation
Impedance tuning will need to be combined with appropriate directional modulation techniques to provide unique directional message transmissions in a system that is optimized for power and reduction of nonlinear distortion. This approach will generate several research challenges that must be overcome for implementation.
The impact of power amplifier nonlinearities on the received messages should be assessed, considered, and mitigated in the optimization algorithms. Because amplifier nonlinearities may cause amplitude and phase distortion to the currents exciting the element antennas, these will result in adjustments to the directional received signals. It is likely that the solutions demonstrated by Rodriguez-Garcia to minimize the undesired spurious beams [15] may also serve a dual purpose of ensuring that the desired antenna currents are realized, but this should be assessed, and solution alternatives should be considered.
Constructing a simulation test bed for assessment and development of array circuit and directional transmission optimization techniques will not be trivial. This simulation test bed must combine the capabilities of signal processing, nonlinear circuit-model simulations, and electromagnetic simulations.
Conclusions
Array impedance tuning and directional modulation have been discussed as complementary solutions allowing better use of spectral and spatial resources in multi-beam radar-communication transmissions. The need for an array capable of multi-beam, directional message transmission, combining high power efficiency with directional signal integrity and security, has been discussed. Developments in the areas of array impedance tuning to maximize the efficiencies of power amplifiers while minimizing unwanted spurious spatial transmissions resulting from amplifier nonlinearities have been overviewed. This technology must be combined with directional modulation, which has been demonstrated to provide multiple signals in multiple directions for joint radar and communications from the same array aperture. To bring these areas together, the impact of impedance tuning on the received directional messages must be considered and mitigated, or appropriate predistortion measures must be employed in real-time to ensure the transmissions are accurate. Solution of this problem will allow efficient, multi-beam directional transmissions from a reconfigurable transmitter power-amplifier array.
ACKNOWLEDGMENTS
This work has been funded by the Army Research Office (Grant No. W911NF-20-2-0270). The views and opinions expressed do not necessarily represent the opinions of the U.S. Government. The authors are grateful to Modelithics for the donation of software component model libraries to Baylor University under the Modelithics University Program, and to Keysight Technologies for the donation of the Advanced Design System and Momentum software to Baylor University.